Below follows the preprint of a discussion in IJSS. Ciavarella’s closure on the discussion is also present on this website and a critical coment on scientific copyright is enclosed.
Some comments on recent generalizations of Cattaneo-Mindlin
by J. Jäger, Lauterbach Verfahrenstechnik, Postfach 711 117, D-76338 Eggenstein, Germany
email: j_jaeger@t-online.de
Copyright © 1999-2001 Elsevier Science.
Preprint for Int. J. Solids & Structures, Feb. 2001, vol. 38, issue 14, pages: 2453-2457.
Version: May, 2000
Abstract: Recently, Dr. Ciavarella published three articles (Ciavarella, 1998a, b, 1999), in which the subject is a theory for frictional contact of equal half-planes and axisymmetric half-spaces, which was previously published by Jäger (1995, 1997a, b). Jäger's solution also covers the case of proportional and incremental loading scenarios. Dr. Ciavarella received these publications in April 1998, but he did not relate his results to Jäger's theory.
In the present note, it is shown that Ciavarella's calculation of the tangential tractions, forces and displacements is not necessary. Furthermore, the example of wedge and conical indenters can be written as a superposition of a Hertzian and a flat profile with rounded corners. The solution for flat rounded profiles was published by Schubert (1942). In the first section of this note, Jäger's theory is shortly summarized. Some comments on Ciavarella's theory for axisymmetric contact follow in Section 2 and the last section treats Ciavarella's theory for plane contact. In order to keep the present note short, we discuss only the surface traction and displacements for a single contact area. Ciavarella's examples for multiple plane contact and the sub-surface stress for axisymmetric contact have not been examined. More remarks can be found in another discussion by Jäger (1999c).
1 Jäger's theory for elastic friction
Historically, the first generalization of Cattaneo-Mindlin was published by Jäger (1995) for axisymmetric contact. From that publication follows the generalization for plane elasticity with multiple contact areas, which was presented at the GAMM-meeting in April 1996 (Jäger, 1997a). It was also shown by Jäger (1999a,b) that this theory can be used for thin and thick layers and some conditions for the generalization of Cattaneo-Mindlin have been presented at the GAMM-meeting (1999d).
In order to simplify Ciavarella's solution, we will summarize the theory by Jäger shortly. For two bodies in contact, the combined displacements are the sum of the displacements of each body. The contact condition for a normal pressure increment is a constant combined displacement of the initial contact area. The stick condition in tangential direction is also a constant rigid body displacement in the stick area. In the slip area, Coulomb's law requires the tangential traction to be proportional to the normal pressure. When the normal and tangential stress-displacement equations are identical, with the exception of a constant factor, each normal solution is also a tangential solution. In this case, the tangential traction q is the difference of the full slip stress of the contact area fp and the slip stress of the stick area fp*, with Coulomb's coefficient of friction f. Variables with asterisk characterize values of the stick area, and the stick areas for increasing tangential forces Q are identical with the contact areas for decreasing normal forces P. The force is an integral of the traction. The tangential displacement at is also proportional to the normal displacement an of the contact area and an* of the stick area, with an appropriate stiffness factor k
![]()
In the case of an axisymmetric contact area with the radius a, all values with asterisk can be written as a function of the radius of the stick area a*, i. e. p*=p(a*). The relation q*=fp* is missing in the mentioned publications by Ciavarella. In the next section, we discuss Ciavarella’s publication on axisymmetric contact.
2 Axisymmetric contact
Ciavarella (1999a) summarized his theory in equations (36) for the corrective shear force and (38) for the tangential displacement, which are identical with equations (34) and (33) by Jäger (1995). For the special case of a flat punch with rounded corners, the gap z1(r) between the surfaces in undeformed contact has the form
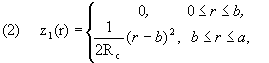
where, Rc, is the rounding radius, b, the radius of the flat area and a, the contact radius. Ciavarella obtained the solution for the normal force P1(a), the normal displacement an1(a) and the pressure p1(a) . We shortly summarize these formulas in a modified form, because they are useful below
![]()
![]()
![]()
![]()
where the variables nk and Gk denote Poisson's ratio and the shear modulus of body k, respectively. It seems that the integral with the term arccos(b/s) in Eq. (5) cannot be expressed with tabulated functions, but it is possible to evaluate the derivative dp(r)/dr. Using integration by parts, the square-root singularity under the integral must first be eliminated. The resulting integral can easily be differentiated, which gives some elliptic integrals listed in Gradstein and Ryshik (1981)
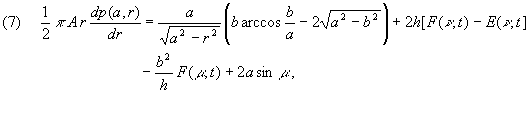
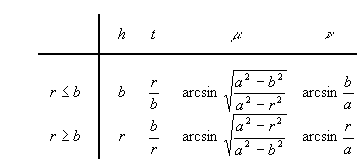
F(n ,t) and E(n ,t) are elliptic integrals of the first and second kind. Equation (6) has the remarkable property that the slope of the pressure is infinite at the border of the flat area (r=b, t=1, m =p /2) and the contact area (r=a) . The first singularity is logarithmic, and is not directly visible in Figures 2 and 3, which Ciavarella (1999) obtained by numerical integration. The integral (5) was also published by Schubert (1942), who presented an approximation for small roundings (a® b), which is identical with the corresponding solution for plane contact.
In section 3.2, Ciavarella discussed the example of a conical punch with rounded tip
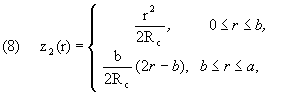
The profile (8) can be written as the difference of a Hertzian profile and a flat punch (2)
![]()
In linear elasticity, solutions can linearly be superposed, and it is not necessary to perform any calculations for the solution of this case. The Hertzian result is the special case b=0 in equations (3), (4). Thus we obtain the result
![]()
![]()
![]()
![]()
where the index 2 characterizes values for the punch with rounded tip and index 1 values from Eqs. (3)-(6). Equations (10)-(13) are identical with Ciavarella's equations (19)-(21). For a < b, the contact area a is smaller than the rounded part b of the tip, and the contact is Hertzian.
In section 4.1, Ciavarella (1999) discussed the tangential solution for a flat punch. Again, there is no necesity for calculation and the results are given by Equation (1). For completeness, we summarize the results shortly
![]()
![]()
![]()
![]()
Equation (17) holds for axisymmetric contact, only. Formulas (14)-(17) can also be used for the conical punch with rounded tip, after substitution of index 2 for 1. Equations (14)-(17) cover all cases of equations (39)-(47) by Ciavarella (1999a).
3 Plane contact
The theory for plane contact with multiples contact areas was reported by Jäger (1997a) and proved in Jäger (1998). Ciavarella (1998a) summarized his theory in equations (18) and (19), which are better expressed with equation (9) q*=fp* by Jäger [1997a]. This relation, and the resulting tangential force Q*=f P* , are missing in Ciavarella (1998a, b). Some examples by Ciavarella (1998b) have also been published by Jäger (1997b), and a comparison of identical formulas is given in the table below
Table of identical formulas by Ciavarella and Jäger
|
Eqs. (22), (23) by Ciavarella (1998b), for the flat punch with rounded corners, have been written in a simpler form by Schubert (1942)
![]()
![]()
![]()
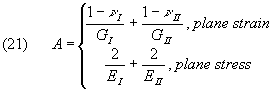
As in the case of axisymmetric contact, the slope of the pressure is infinite at r=b. The solution for a wedge with rounded apex is the difference of a Hertzian profile and a flat punch (18)-(20)
![]()
![]()
with H(x) given by (13) and P1(a), p1 (a,x) by (18)-(20). Again, the tangential solution for symmetric profiles follows from equations (14)-(17), with k =1 for plane contact. The displacements can only be determined relative to a reference point, as usual for half-planes.
It should be noted that Ciavarella’s equation (A9) has the wrong dimension and becomes singular for odd k. It should be replaced with equation (18) by Jäger [1997b]
![]()
with the hypergeometric function F(a,b;c;x).
Ciavarella [1998a-I] distinguishes on page 2355 among known or unknown contact areas, but only the profile is known, a priori. When the profile has edges with vertical or concave tangents, such edges are a border of the contact area. In this case, a rigid body displacement in form of a flat punch solution with sharp edges can be superposed. When the slope of the profile is finite and convex, the pressure falls to zero at the border of the contact area.
The remarks on page 2356 by Ciavarella [1998a-I] should be replaced with the following
- The corrective shear traction q* is always the full slip stress fp* of the stick area.
- The stick condition is a constant rigid body displacement, and therefore, identical only with the contact condition, when the bodies do not rotate. Consequently, the bodies must not rotate during tangential loading.
- For contact profiles with flat areas of different height, higher areas enter in contact with increasing normal forces and the new contact areas change their form with the compression. When a tangential force is applied, a slip area propagates at the highest flat area and a partial slip solution exists. Only when all flat areas have the same height, all contact areas stick completely for forces below Coulomb's limit.
Finally, it can be concluded from the pressure (7), (18) for flat rounded punches that a discontinuous second derivative of the displacement produces an infinite slope of the pressure.
References
Ciavarella, M., 1998a, The generalized Cattaneo partial slip plane contact problem, I - Theory, Int. J. Solids Stuctures, Vol. 35, 2349-2362.
Ciavarella, M., 1998b, The generalized Cattaneo partial slip plane contact problem, II - Examples, Int. J. Solids Stuctures, Vol. 35, 2363-2378.
Ciavarella, M., 1999, Indentation by nominally flat or conical indenters with rounded corners, Int. J. Solids Structures, Vol. 36, 1999, 4149-4181.
Gradstein I. S., Ryshik I. M., 1981, Tables of series, products and integrals, Verlag Harri Deutsch, Thun-Frankfurt/M.
Jäger, J., 1995, Axisymmetric bodies of equal material in contact under torsion or shift, Arch. Appl. Mech., Vol. 65, 478-487.
Jäger, J., 1997a, Ein neues Prinzip der Kontaktmechanik, Z. angew. Math. Mech., Vol. 77, S143-S144, presented at the GAMM-meeting in April 1996.
Jäger, J., 1997b, Half-planes without coupling under contact loading, Arch. Appl. Mech., Vol. 67, 247-259.
Jäger, J., 1998, A new principle in contact mechanics, J. Tribology, Vol 120, 677- 685.
Jäger, J., 1999a, Equal layers in contact with friction, Contact Mechanics IV, eds.: Gaul, L., Brebbia, C.A., WIT-Press, Southampton, 99-108.
Jäger, J., 1999b, A generalization of Cattaneo-Mindlin for thin strips, J. Appl. Mech., Vol. 66, 1034-1037.
Jäger, J., 1999c, Discussion of: Tangential loading of general 3D-contacts, J. Appl.Mech., Vol. 66, 1048-1049
Jäger, J., 1999d, Conditions for the generalization of Cattaneo-Mindlin, presented at the GAMM-meeting 1999, ZAMM, in press.
Schubert, G., 1942, Zur Frage der Druckverteilung unter elastisch gelagerten Tragwerken, Ing. Arch., Vol. 13, 132-161.