Analytical Solution of Contact Impact Problems
by J. Jaeger, Blattwiesenstr. 7, D-76227 Karlsruhe, Germany.
Appl. Mech. Rev., 1994, Vol. 47, pp. 35-54
email: j_jaeger@t-online.de
Contents of selected sections
1 Summary: In this article, analytical solutions of the normal and tangential impact of half-spaces at low velocities are formulated. After a brief introduction, a classification of contact problems is proposed and some publications about impact are mentioned. The basic contact laws for monotonously increasing normal, tangential, and torsional contact have been found decades ago, while the general analytical solutions for tangential and torsional load histories, which are necessary for impact calculations, have only been found recently. Insertion of these contact laws into the equations of motion yields a system of nonlinear differential equations, which are uncoupled in the case of the oblique central impact. The normal solution of the uncoupled equations for Hertzian and some axisymmetric surfaces can be written as a hypergeometric function, which generalizes earlier solutions. Solutions in tangential direction for the compression phase and the restitution phase can be found for the case of complete adhesion. Finally, the kinematic coefficient of restitution is shown. This solutions may help to understand some open problems of the collision of rigid bodies, which are in contact on a small elastic domain, where a part of the kinetic energy is transformed into elastic energy and reconverted into kinetic energy in normal and tangential directions.
2 Introduction
Johnson [1985] wrote in his book, `The subject of contact mechanics may be said to have started 1882 with the publication by H. Hertz of his classic paper On the contact of elastic solids'. Hertz found a contact law of a simple analytical form for the compression of equal bodies, which was confirmed by many experiments (Goldsmith [1960]). Based on the observation that the quasi-static contact theory is restricted to small relative velocities, progress in contact impact has been largely associated with the investigation of elastic-plastic stress waves. Furthermore, the argument of Hertz in his paper, that the elastic waves during impact must be reflected many times in the bodies in order to assure quasi-static contact, supported the wave theory of impact. This argument is certainly true for the longitudinal impact of thin rods, which behave like heavy linear springs left in a state of vibration after impact. It is not true, however, during the impact of a rigid sphere on an infinite elastic half-space, where no waves are reflected at all. This contradiction was eliminated by the papers of Eason [1966] and Hunter [1957]. Eason [1966] calculated the displacements of an elastic half-space produced by a suddenly applied surface force, in the form of a spherical or constant pressure distribution, acting on a circular area of diameter 2a. He found that the displacement of the surface in the center of the loaded region reaches its statical equivalent value after the time t
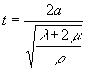 (1)
(1)
l, m = Lam'e's constants , r= density ,
which compressive waves need to travel through the loaded area. Hunter [1957] calculated the energy loss produced by elastic waves during the impact of a sphere on an elastic half-space. The fraction of the energy loss in the half-space and the initial kinetic energy of the sphere has the value
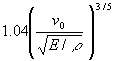 (2)
(2)
E : Young's modulus .
This energy loss is negligible, as long as the initial velocity v0 of the sphere at the beginning of the impact is small compared with the velocity of elastic waves in thin elastic rods. This condition is much less restrictive than the assumption of Hertz (Johnson [1985]).
The first studies of elastic contact under the influence of tangential forces were published by Cattaneo [1938] and Mindlin [1949]. The Cattaneo-Mindlin contact law is also confirmed by experiments (Mindlin et al. [1952], K. L. Johnson [1955], [1985] ). It is restricted to monotonously increasing tangential forces and constant normal compression and could therefore not be applied to the tangential impact. Until today, many authors tried to find a more general contact law (Mindlin & Deresiewicz [1953], Dobry et al. [1991], Mroz & Stupkiewicz [1992]), especially for granular material (Deresiewicz [1958]). In a paper by Michalowski & Mr'oz [1978] an analogy to plasticity relations for hardening and softening materials was used to derive so-called associated and non-associated sliding rules in contact friction problems. Therefore a general contact law for tangential forces was developed by the author and presented in this article. The analytical solution for tangential contact of non-Hertzian surfaces is still open.
The Cattaneo-Mindlin theory is restricted to elastically similar materials based on the half-space theory. If the materials are dissimilar, the load displacement equations in the normal and tangential direction are coupled and application of a normal pressure distribution produces tangential displacements and vice versa. The normal loading of two elastically dissimilar bodies was first studied by Mossakovski [1963], who calculated the associated tangential stress by an incremental technique. The normal contact of dissimilar spheres without slip has been analysed by Goodman [1962] on the basis of neglecting the influence of tangential traction on normal pressure. Spence [1968] pointed out that the stress field of axisymetric contact problems with normal loading depends only on the contact radius, so that an appropriate normalization must yield solutions which are independent of the contact size. Therefore, the stress field at all stages of loading must be independent of the normal load history, i. e. the solution is self-similar and a non-incremental technique can be used. The frictional unloading problem was solved numerically by Turner [1979]. Because, of the difficulties of analytical solutions, the normal impact of dissimilar spheres was solved numerically by Jaeger [1992]. The contact law was calculated by discretization of the load-displacement integrals of the half-space and the differential equations of motion were integrated by finite increments. It should be noted that calculation time and computer memory can be saved by consideration of symmetries of the discrete load-displacement matrix and that inversion of this matrix can be avoided using an adapted form of the Gauss- Seidel method. Based on this ideas contact areas with up to 1000 points can be calculated, using 80386 processors and conventional MS-DOS with 640 kByte memory, although the complete load displacement matrix in double precision alone occupies 32x10002x8=72 Megabyte memory (Jaeger [1992]). It should also be noted that FEM calculations require the discretization of the entire body outside of the contact area and under the contact area, which amounts to at least one million (106) nodes for a contact area of 1000 points, with nonlinear incremental contact conditions. Progress on the field of BEM in Contact Mechanics is reported in publications by Karami [1989], Man et al. [1993] and Aliabadi & Brebbia [1993].
Although several analytical solutions exist for normal impact, there is only one publication by Maw et al. [1981] about the effect of frictional elastic forces on the tangential impact. Maw et al. solved the impact problem numerically and compared the solution with experiments. Analytical solutions can be found in the case of complete adhesion; some results are presented in this paper. The general tangential impact with partial slip can only be solved numerically (Jaeger [1992], [1993c]). The classical theory of Poisson [1833] and Routh [1860] assumes either gross slip with Coulomb's law for sliding or complete adhesion with ideal-plastic adhesion in tangential direction. In normal direction, on the other hand, an elastic-plastic material law is assumed, with varying coefficients of restitution. Thus elastic material behaviour is only allowed in normal direction but not in tangential direction. Hor'ak [1931] considered the elastic behaviour in tangential dirction using a coefficient of restitution in matrix form. A publication by Stronge [1990] generalized Newton's coefficient of restitution for the planar impact with friction, retaining the assumptions of Poisson and Routh. In the last months several publications appeared about rigid body collisions with friction, which indicates that this problem is still open. The papers by Brach [1993], Smith et al. [1992], Ivanov [1992] discuss the hypothesis of Stronge, while a paper by Wang et al. [1992] discusses Poisson's hypothesis - i. e. the ratio of the impulse in the period of compression to the period of restitution - versus Newton's hypothesis.
Some approximations for viscoelastic impact (Hunter [1960]) and plastic impact have been published, which are commented in Johnson [1985]. Because of the complexity of contact-impact problems, this article is only dedicated to elastic impact.
3 Classification and Literature Survey
The literature about contact problems is very extensive and manifold, because the geometry and the physical behaviour of the bodies can not be described by a simple model, like e. g. the beam theory for one dimensional structures under plane stress. Several methods of solutions have been developed, which can be adapted to special problems; for example H. Hertz [1882] idealized the contacting objects as rigid bodies with a local elastic domain in the vicinity of the contact region, while a theory by F. Neumann [1885] and St. Venant [1862] analysed the propagation of one dimensional elastic waves during the longitudinal impact of beams. In the first part of this section we classify the contact problems by division into nine groups:
1. Global form of the bodies:
a) Massive 3-dimensional bodies with uniform geometry (e. g. half-spaces).; b) Massive bodies with complex geometry; c) layered solids, plates and shells; d) 2-dimensional structures (e. g. plates, shells); e) 1-dimensional bodies (e. g. beams, shafts); f) other.
2. Local surface in the vicinity of the contact region:
a) Paraboloids (e. g. Hertzian surfaces); b) blunt wedges and cones; c ) high order polynomials (e. g. rn); d) conforming surfaces (e. g. an elastic sphere indenting an elastic cavity, a flat punch indenting a half-space); e) asperity contact; f) other.
3. Symmetries:
a) Plane stress or plane strain; b) axi-symmetry; c) Hertzian surfaces (e. g. elliptical contact regions); d) no symmetries; e) other.
4. Material:
a) Elastic, isotropic, homogeneous; b) linear visco-elastic; c) plastic; d) tangential plasticity; e) other (e. g. anisotropic, inhomogeneous).
5. Direction of loading:
a) Normal loading; b) tangential loading (e. g. unidirectional partial slip, torsion); c) coupling of normal and tangential loading (e. g. Goodman approximation); e) other.
6. History of loading and kinematics:
a) Static displacement; b) quasistatic increments (e. g. impact at low velocites); c) steady rolling; d) transient rolling; e) wave propagation ( e. g. high velocity impact, detonations); e) other.
7. Method of analysis:
a) Analytical; b) BEM (e. g. Boundary Element Method, Boundary Integral Method ); c) FEM: Finite Element Method; d) experiment; e) other.
8. Local frictional law:
a) Coulomb-Amontons law with equal static and kinetic coefficient; b) Coulomb-Amontons law with different coefficients; c) complete adhesion; d) molecular adhesion; e) fluid lubrication; f) other.
9. Miscellaneous:
a) Thermoelastic contact; b) contact stability; c) dynamic buckling; d) large deformations; e) granular material.
The first group classifies the global form of the bodies, which determines the elastic compliance and stiffness under the action of loading. In the case of elastic materials the general displacement can be described as a superposition of single force solutions or influence functions. If the geometry is uniform, the single force displacement is independent of the position of the force, which simplifies the numerical procedure. The most important analytical solutions are based on the half-space theory (Hertz [1882], Cattaneo [1938], Mindlin [1949]), which is adequate for massive bodies. The second group describes the local geometry about the contact region, in which the normal displacement is prescribed. The half-space theory is suited for massive bodies 1a with nonconfor ming surfaces 2a-c, but not for conforming bodies 2d. The symmetries of group three simplify the mathematical solution of the problem. The classification of group four concerns the material properties. Most analytical solutions belong to category 4a; only special analytical solutions are known for inelastic material 4b-c. Category 4d denotes the classical impact theory with friction, where point contact was assumed with tangential plasticity at low velocities (i. e. the Routh-Poisson hypothesis, Routh [1860]). The direction of loading in group five classifies special solutions like Hertzian normal loading of half-spaces, for example, which belongs to category 5a. Case 5c of normal and tangential coupling is more difficult. Such a coupling can be an inherent characteristic of the influence functions, like the load displacement integrals of half-spaces for dissimilar materials, or a kinematical condition of the loading mechanism, like oblique impact of nonspherical bodies.
Group six classifies the kinematical process of loading. This article is mainly concerned with low velocity impact problems of category 6b. The classical laws of impact by Galilei [1638], Newton [1686], Marci [1639], Huygens [1669], etc. furnished a theory of frictionless impact, which is well established, while the analysis of the elastic impact with friction has been developed only recently (Maw et al.[1976], Jaeger[1992]). Since a general theory is still in progress, we will discuss some recent solutions in this field. Low velocity impact belongs to category 6b and can be regarded as a sequence of static increments, based on the solutions of category 6a. The problems of category 6c `Steady rolling' and 6d `Transient rolling' are treated in an excellent book by J. J. Kalker [1990], who developed a variational theory of frictional contact and numerical algorithms for frictional half-space problems (categories 1a&c, 4a-b, 6a-d, 7b). Group seven distinguishes basically analytical, numerical, and experimental methods. The local frictional law is distinguished in section eight. Analytical solutions are usually based on category 8a, because different coefficients of static and dynamic friction render complicated integral equations, which are too difficult for analytical methods. Complete adhesion of category 8c signifies that no slip takes place in the whole contact area. In the ninth group, miscellaneous problems are distinguished. It should be noted that this classification can only be temporary, because different fields of research and scientific progress require different classifications.
The global behaviour of impacting objects can be described by the equations of motion, while the contact force depends on the local contact law. It is therefore necessary to study contact mechanics, in order to describe the impact process correctly. The first book about contact problems was published by Galin [1953]. It treats mainly plane and elliptical contact problems 1a, 3a-c, plane and rotational symmetric problems with friction 3a-b, 5c, 8a, etc. The methods are based on Muskhelishvilli's works [1953, 1992]. Later, Gladwell [1980] published a book about contact problems, which discusses also mostly plane and rotational symmetric problems (1a-d, 3a-c, 6a, 7a, 8a) and contains a chapter about three-dimensional contact problems. The already classical book `Contact Mechanics' by Johnson [1985] provides an excellent survey about the state of the art. It contains plastic and viscoelastic materials (4a-c) and discusses static loading, rolling, and wave propagation (6a-e). A book by Barber [1992] treats two- and three-dimensional contact problems, thermoelasticity, and interface cracks. Analytical results for the interior stress field of various plane and axi-symmetric problems are listed in the book `Mechanics of contact impact' by D. A. Hills, D. Nowell, A. Sackfield [1993] ( categories 1a-b, 2a-b, 3a-c, 4a, 5a-c, 6a&c, 7a, 8a). Basic knowledge about fluid lubrication is summarized in `Tribology: Principles and Design Applications' by Arnell et al. [1991]. The volume `Boundary Value Problems in Linear Viscoelasticity' by Golden & Graham [1988] treats viscoelastic contact problems with friction.
Four books have been published about impact problems. The first one is titled `Impact: The theory and physical behaviour of colliding solids' by Goldsmith [1960] and treats mainly vibrational aspects (categories 6e) of elastic, viscoelastic and plastic impact (categories: 1b-c, 2a, 4a-c, 5a, 6e, 7a). The second book `Impact strength of materials' by W. Johnson [1972] is also dedicated to elastic-plastic wave propagation, though on a simpler level as Goldsmith. The third book `Impact dynamics' by Zukas et al. [1979] discusses again elastic-plastic wave propagation, ballistics, projectile penetrations, and computational methods for high velocity impact. These three books are mainly dedicated to the wave propagation in one- and two-dimensional structures, according to the theory of Neumann and St. Venant. In this case the wave front is planar or circular, in contrast to spherical waves, which propagate into massive bodies. Spherical waves decrease rapidly with increasing depth of penetration, which justifies the quasi-static theory of H. Hertz. The only book about low velocity impact of compact bodies is titled `Mechanical Impact Dynamics: Rigid Body Collisions' by R. M. Brach [1991], who introduced normal and tangential coefficients of restitution, in order to determine he global behaviour of the bodies. These coefficients must be measured empirically. Only the Hertzian contact law is studied in theses books.
There are also some interesting survey articles about impact. The article `Der Stoá' by Th. Pschl [1926] describes the theory of Hertz, Neumann, and St. Venant. Barkan [1974] discusses the quasistatic impact of spheres and wave propagation in bars. Finally, the article `Aspects of Contact Mechanics' by Kalker [1975] is an interesting survey about the state of the art at that time, with special attention to unsolved problems.
The historical development of mechanics and the history of impact from the ancient greeks to H. Hertz is outlined in a philosophical work by E. Mach [1912]. Furthermore Istv'an Szab'o [1977] published a book about the history of mechanics, which includes a chapter about the history of impact from Galilei to Timoshenko.
Only a few closed form analytical solutions of impact problems have been found, mostly based on a half-space contact law. In the next section we present the load displacement relations for the elastic half-space.
References
Abramowitz, M., Stegun, I., 1972, Handbook of mathematical functions, Dover Publications, New York.
Aliabadi, M. H., Brebbia, C. A. (editors), Computational Methods in Contact Mechanics, Computational Mechanics Publications, Elsevier Applied Science, 1993.
Arnell, R. D., Davies, P. B., Halling, J., Whomes, T. L., 1991, Tribology: Principles and Design Applications, Macmillan, London.
Barber, J. R., 1992, Elasticity, Kluwer, Dordrecht.
Barber, J. R., 1979, Adhesive contact during the oblique impact of elastic spheres, J. Appl. Math and Phys. (ZAMP), Vol. 30, 468-476.
Barkan, P., 1974, Impact, Mechanical Design and Systems Handbook, Ed.: H. A. Rothbart, Section 16, McGraw-Hill, New York.
Boussinesq, J., 1885, Application des Potentials `a l''etude del 'equilibre et du mouvement des solides 'elastiques, Paris: Gauthier-Villars.
Brach, Raymond M., 1993, Classical planar impact theory and the tip impact of a slender rod, In. J. Impact Engng., Vol. 13, pp. 21-33.
Brach, Raymond M., 1991, Mechanical Impact Dynamics: Rigid Body Collisions', John Wiley & Sons, New York.
Bronstein, I. N., Semendjajew, K. A., 1979, Taschenbuch der Mathematik, Verlag Harri Deutsch, Frankfurt.
Cattaneo, C., 1938, Sul contatto di due corpi elastici: distribuzione locale degli sforzi, Rendiconti dell' Accademia nazionale dei Lincei, 27, Ser. 6.
Cerruti, V., 1882, Roma, Acc. Lincei, Mem. fis. mat.
Deresiewicz, H., 1968, A note on Hertz's theory of impact, Acta Mech., Vol. 6, 110.
Deresiewicz, H., 1958, Mechanics of granular matter, in: Advances in Applied Mechanics, eds.: Dryden, Karman, Kuerti, New York, Vol. V, p. 233-305.
Deresiwicz, H., 1954, Contact of elastic spheres under an oscillating torsional couple, J. Appl. Mech., Vol. 21, 52-56.
Dobry, R., Ng, T. T., Petrakis, E., Seridi, A., 1991, General model for contact law between two rough spheres, J. Eng. Mech., ASFE, Vol. 117, 1365-1381.
Galilei, G., 1638, `Unterredungen und Demonstrationen ber zwei neue Wissenszweige', Ostwald's Klassiker, No. 25, 38, Leipzig, Engelmann, 1890- 91.
Galin, L. A., Kontaktnye Zadachie Teorii Uprugosti, Gostekhizdat; engl. trans. by H. Moss, 1961, ed.: I. N. Sneddon, Contact problems in the theoriy of elasticity, North Carolina State College.
Gladwell, G. M. L., 1980, Contact problems in the classical theory of elasticity, Sijthoff & Noorhoff, Alphen aan den Rijn, The Netherlands.
Golden, J. M., Graham, G. A. C., 1988, Boundary value problems in linear viscoelasticity, Springer, Berlin etc.
Goldsmith, Werner, 1960, Impact: The theory and physical behaviour of colliding solids, Edward Arnold Ltd., London.
Graham, G. A. C., 1973, A contribution to Hertz's theory of elastic impact, Int. J. Engng. Sci., Vol 11, 409-413.
Horak, Z., 1931, Th'eorie g'en'erale du choc dans les syst`emes mat'eriels, J. 'ecole polytech., Ser. 2, Vol 28, 15.
Hunter, S. C., 1957, Energy absorbed by elastic waves during impact, Journal of Mechanics and Physics of Solids, 5, 162.
Hunter, S. C., 1960, The Hertz problem for a rigid spherical indenter and a viscoelastic half-space, J. Mech. Phiys. olids, Vol. 8. pp 219-234.
Huygens, C., 1669, Oeuvres Compl`etes, publi'ees par la Societ'e hollandaise des Sciences, 16, Percussion, The Hague, M. Nijhoff, 1929.
Ivanov, A. P., 1992, Energetics of a collision with friction, J. Appl. Maths. Mechs., Vol. 56, No. 4, pp. 527-534
Jaeger, J., 1993a, Torsional load-histories of elastic spheres in contact, in:Contact Mechanics, eds.: M. H. Aliabadi, C. A. Brebbia, Computational Mechanics Publications, Southampton, 1993.
Jaeger, J., 1993b, Elastic contact of equal spheres under oblique forces, Arch. Appl. Mech., Vol. 63, no. 6, 402-412, 1993.
Jaeger, J., 1993c, Oblique impact of similar bodies with circular contact, Report at the GAMM-Seminar Kontakt fester Körper, Universität Stuttgart, Institut für Mechanik (Bauwesen), March 18-19, 1993, accepted for publication in Acta Mechanica.
Jaeger, J., 1992, Elastic impact with friction, Thesis, Delft, Technical University. Johnson, K. L., 1985, Contact mechanics, Cambridge University Press, Cambridge.
Johnson, K. L., 1955, Surface interaction between elastically loaded bodies under tangential forces, Proceedings of the Royal Society, A230, 531.
Johnson, W., 1972, Impact strength of materials, Edward Arnold Ltd., London.
Kalker, J. J., 1975, Aspects of Contact Mechanics, in: The mechanics of the contact beween deformable bodies by A. D. de Pater and J. J. Kalker, Proceedings, Delft University Press, Delft.
Kalker, J. J., 1990, Three-dimensional elastic bodies in rolling contact, Kluwer Academic Publishers.
Karami, G., 1989, A Boundary Element Method for two-dimensional contact problems, (Lecture Notes on Engineering 51), Springer, Berlin etc.
Love, A. E. H., 1939, Boussinesq's problem for a rigid cone, Quarterly Journal
of Mathematics (Oxford series), Vol 10, 161.
Lubkin, J. L., 1951, Torsion of elastic spheres in contact, J. Appl. Mech., ASME, 18, 183.
Mach, Ernst, 1912, Die Mechanik in ihrer Entwicklung, Leipzig, Brockhaus; english ranslation: The science of mechanics by Ernst Mach, Chicago, The Open Court Publishing Co.
Man, K. W., Aliabadi, M. H., Rooke, D. P., 1993, Frictional contact analysis using boundary element method, pp 164-173, in: Contact Mechanics, eds.:
M. H. Aliabadi, C. A. Brebbia, Computational Mechanics Publications, Southampton, 1993.
Marci, M., 1639, De Proportione Motus, Prague.
Maw, N., Barber, J. R., Fawcett, J. N., 1981, The role of tangential comliance in oblique impact, Journal of Lubrication Technology, Trans. ASME, Seris F, 103, 74-80.
Maw, N., Barber, J. R., Fawcett, J. N., 1976, The oblique impact of elastic spheres, Wear, 38, 101.
Michalowski, R., Mr'oz, Z., 1978, Archives of Mechanics, Warszawa, Vol. 30, ser. 3, pp. 259-276.
Mindlin, R., 1949, Compliance of elastic bodies in contact, J. Appl. Mech., Trans. ASME, 16, 259.
Mindlin, R. D., Mason, W. P., Osmer, J. F., Deresiewicz H., 1952, Effects of an oscillating tangential force on the contact surfaces of elastic sheres, Proc. 1st US National Congress of Applied Mechanics, p. 203, New York: ASME.
Mindlin, R., Deresiewicz, H., 1953, Elastic spheres in contact under varying oblique forces, J. Appl. Mech., Trans. ASME, 20, 327.
Mossakovski, V. I., 1963, Compression of elastic bodies under conditions of adhesion, 27, 418.
Mroz, Z., Stupkiewicz, S., 1992, Constitutive modelling of slip and wear in elastic, frictional contact, in: Proc. Contact Mechanics Int. Symp., edt. by A.
Curnier, Presses polytechniques et universitaires romandes, Lausanne, pp. 133-156.
Muskhelishvilli, N. I., 1953, Some basic problems of the mathematical theory of elasticity, transl. by J. R. M. Radok, Noordhoff, Groningen.
Muskhelishvilli, N.I., 1992, Singular Integral Equations, trans. by J. R. M. Radok, Dover Publications, New York, (rebublication of the edition from 1953, Noordhoff, Groningen).
Neumann, Franz, 1885, Vorlesungen ber die Theorie der Elastizitt, Kap. 20, Leipzig, lectures given 1857/1858.
Newton, I., 1686, Philosophiae naturalis principia mathematica, egl. trans. by A. Motte, New York, D. Adee, 1848.
Pöschl, T., Der Stoss, handbuch der Physik, 6, Chapter 7, Springer, Berlin.
Poisson, S. D., 1833, Trait'e de m'ecanique, Bachelier, Paris.
Ramsauer, C., 1909, Experimentelle und theoretische Grundlagen des elastischen und mechanischen Stosses, Ann. Phys. Chem. (Poggendorf), 30, Ser. 7.
St.-Venant, Barr'e de, 1862, Journal des Math'ematiques, Ser. 2, Vol. 12, 237-376.
Routh, E. J., 1860, Dynamics of a System of Rigid Bodies: Elementary Part, 7th ed., Macmillan, London; also, Dover Publications, New York, 1905, pp. 126-162
Smith, Charles E., Liu, Pao-Pao, 1992, Coefficients of Restitution, J. Appl. Mech., ASME, Vol. 59, pp. 963-969.
Spence, D. A., 1968, Self-similar solutions to adhesive contact problems incremental loading, Proc. R. Soc. Lond., A305, 55.
Steuermann, E., 1939, On Hertz theory of local deformations of compressed bodies, Comptes Rendus (Doklady) de l'Acad'emie des Sciences de l'URSS, 25, 359
Stronge, W. J., 1990, Rigid body collisions with friction, Proc. R. Soc. Lond., A431, pp. 169-181.
Szab'o Istv'an, 1977, Geschichte der mechanischen Prinzipien und ihrer wichtigsten Anwendungen, Birkhuser, Basel.
Turner, J. R., 1979, The frictional unloading problem on linear elastic half-space, ournal of Institue of Mathematics and its Applications, 24, 439.
Vermeulen, P. J., Johnson, K. L., 1964, Contact of non-spherical elastic bodies transmitting tangential forces, J Appl. Mech., Trans. ASME, 31, 338.
Wang, Y., Mason, M. T., 1992, Two-dimensional rigid-body collisions with friction, J. App. Mech., Vol. 59, pp. 635-642.
Wittenburg, J., 1977, Dynamics of systems of rigid bodies, Teubner, Stuttgart.
Zukas, J. A., Nicholas, T., Swift, H. F., Greszczuk, L. B., Curran, D. R., 1982,
Impact Dynamics, John Wiley & Sons, New York.